Article Text
Abstract
Objectives To systematically assess the robustness of meta-analyses based on randomised controlled trials (RCTs) in vascular surgery using the Fragility Index (FI).
Design Cross-sectional study.
Setting Meta-analyses published in English from January 2019 to April 2025, identified from EMBASE, PubMed and Web of Science.
Participants 67 articles, with 291 meta-analyses involving RCTs evaluating vascular surgical interventions, covering venous, aortic, peripheral arterial, vascular access and other relevant fields.
Main outcome measures FI, defined as the minimum number of event changes required to alter the statistical significance of meta-analysis results, and its association with sample size and total number of events, analysed using frequency distribution histograms and restricted cubic spline models.
Results The median FI was 7, with considerable variation across different fields. Aortic meta-analyses demonstrated higher robustness compared with venous and vascular access meta-analyses. FI showed a non-linear relationship with sample size and total number of events, indicating robustness improved only up to specific thresholds, beyond which robustness declined or plateaued.
Conclusion Overall robustness of meta-analyses in vascular surgery was moderate, with notable variability among research areas. FI provides valuable insight into the stability of synthesised evidence, suggesting the need for improved methodological quality and advocating broader adoption of FI in meta-analytical research.
- Clinical Decision-Making
- Cardiovascular Disease
- Vascular surgery
- Meta-Analysis
Data availability statement
Data are available upon reasonable request. All data relevant to the study are included in the article or uploaded as supplementary information. All of the data were publicly available data and researchers interested in our study should contact the corresponding author at guoyi0426@qq.com by providing specific ideas.
This is an open access article distributed in accordance with the Creative Commons Attribution Non Commercial (CC BY-NC 4.0) license, which permits others to distribute, remix, adapt, build upon this work non-commercially, and license their derivative works on different terms, provided the original work is properly cited, appropriate credit is given, any changes made indicated, and the use is non-commercial. See: http://creativecommons.org/licenses/by-nc/4.0/.
Statistics from Altmetric.com
STRENGTHS AND LIMITATIONS OF THIS STUDY
Comprehensive literature search from three major databases ensured broad inclusion of recent vascular surgery meta-analyses.
Fragility Index calculation used a standardised, validated online tool, ensuring consistency and reproducibility of robustness assessment.
Restricted cubic spline analyses effectively modelled complex, non-linear relationships between robustness and key methodological parameters.
The Fragility Index does not account for between-study heterogeneity or publication bias, potentially limiting the interpretation of robustness.
Inability to incorporate risk-of-bias assessments of primary randomised controlled trials due to inconsistent reporting methods across included meta-analyses.
Introduction
Meta-analysis is a statistical method employed in systematic reviews to synthesise the results of multiple studies, thereby enhancing statistical power and providing a single quantitative estimate.1 Meta-analyses based on randomised controlled trials (RCTs) are widely considered the highest level of evidence for evaluating therapeutic efficacy. In recent years, the number of published meta-analyses has increased sharply. However, the methodological quality and consistency of reporting vary markedly across studies, which may ultimately influence clinical guidelines and decision-making.2
Several standardised tools are available for appraising meta-analyses. The Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) statement offers a 27-item checklist designed to promote transparent reporting of methods and findings,3 while A MeaSurement Tool to Assess systematic Reviews 2 (AMSTAR 2) assesses methodological rigour and risk of bias (RoB) in review processes.4 However, neither tool evaluates the robustness of study outcomes.
In individual RCTs, the Fragility Index (FI) has been proposed as a metric of statistical robustness. It represents the minimum number of participants whose outcome status would need to be changed from a non-event to an event to alter the results from statistically significant to non-significant.5 For non-significant results, a related metric, the reverse Fragility Index (RFI), has been introduced to indicate how many event changes would be necessary to be statistically significant.6 A small FI suggests that the result is statistically fragile and may lack clinical reliability. These tools have been employed to assess the robustness of trial findings across various specialties, including vascular surgery.7
Recognising the value of this approach, Atal et al have extended the application of FI to meta-analyses based on RCTs with binary effect estimates, such as risk ratio (RR), OR and risk difference (RD). In this context, the FI denotes the minimum number of event changes across the included trials required to alter the statistical significance of the pooled result, irrespective of whether the original finding is statistically significant or not.8 This unified approach has gained traction across clinical fields such as cardiovascular medicine9 and paediatrics,10 enabling clearer interpretation of synthesised evidence.
In vascular surgery, the number of meta-analyses has increased rapidly. While this trend reflects a growing interest in evidence synthesis, the overall quality of these studies remains inconsistent. Systematic reviews in this field often display shortcomings in reporting, protocol registration and RoB evaluation.11 Furthermore, meta-analyses addressing similar topics often yield divergent results due to methodological inconsistencies and variations in data quality, undermining their reliability for clinical application.
Despite growing awareness of the importance of robustness, few studies have systematically assessed the FI of meta-analyses in vascular surgery or explored the influencing factors. To address these gaps, the present study aims to: (1) comprehensively identify RCT-based meta-analyses in vascular surgery published in the past 5 years; (2) calculate their FIs based on binary effect estimates; (3) analyse how robustness correlates with sample size and total number of events using restricted cubic spline (RCS). By evaluating the structural stability of vascular surgery meta-analyses, this study seeks to improve confidence in synthesised evidence and enhance its clinical utility.
Methods
This work was reported in line with the PRISMA statement.3 Please see the checklist in online supplemental table A1.
Supplemental material
Patient and public involvement
Patients or the public were not involved in the design, or conduct, or reporting, or dissemination plans of our research.
Search strategy
Computerised search was conducted in EMBASE, PubMed and Web of Science, along with manual retrieval, with language restricted to English, to comprehensively collect meta-analyses published of vascular surgery over the past 5 years, using the terms (“meta analy*” OR “metaanaly”) AND (“Aortic Aneurysm” OR “Aneurysm, Dissecting” OR “Aneurysm, False” OR “arteriosclerosis obliterans” OR “thromboangitis obliterans” OR “arterial embolism” OR “Carotid artery stenosis” OR “mesenteric ischemia” OR “peripheral artery disease”). The time frame of the search was published between 1 January 2019 and 7 April 2025. Please see the search strategy in online supplemental table A2.
Inclusion and exclusion criteria
Inclusion criteria
Study type: RCT-based meta-analyses. If a meta-analysis included both observational studies and RCTs but conducted subgroup analyses based on study types, only the results of the RCT subgroup would be included.
Interventions or controls: the meta-analyses were required to focus on vascular surgical interventions or comparators, such as thoracic endovascular aortic repair, endovascular aneurysm repair, carotid artery stenting and similar procedures.
Pooled effect measures: the pooled effect measures in the study were required to be either OR, RR or RD.
Exclusion criteria
Study type: network meta-analyses or meta-regression analyses were excluded.
Literature content: articles with incomplete information, such as those not specifying the pooled method or having incomplete forest plot data with missing values, would be excluded.
Others: retracted articles, published errata or earlier versions of updated articles were excluded.
Literature selection
The retrieved literature was imported into EndNote X9 for reference management. Two researchers (JL and CW) independently screened the titles and abstracts, followed by a review of the full texts of relevant publications to determine eligibility. Any discrepancies in literature selection were resolved through consultation with the senior investigator (YG).
Data extraction
Two researchers (TW and WL) independently extracted the following information using a predefined data collection sheet: title, year of publication, study field, journal, intervention, control, outcome, sample size and number of events for each group in the paired comparisons, the pooled effect measures, the pooled effect size, the width of CI, method used, model used. All of the above data were publicly available and did not require ethical committee approval.
Fragility Index calculation
FIs were calculated using the online calculator (https://clinicalepidemio.fr/fragility_ma/) developed by Atal et al.8 This method is specifically designed for meta-analyses based on binary outcomes and does not differentiate between statistically significant and non-significant results, thereby providing a unified approach to evaluating robustness.
For example, in a meta-analysis containing n trials with RR as the effect measure, the FI is calculated as follows. Suppose the meta-analysis compares two treatments (A and B), where the incidence in Group A is lower than in Group B and the result is statistically significant (eg, the upper limit of CI for RR I less than 1). To determine the FI (eg, the minimum number of event modifications required to render the result non-significant), the event status of participants is iteratively altered across all included trials.
Specifically, while keeping the total number of participants in each group unchanged, one participant in Group A whose event originally ‘did not occur’ is changed to ‘occurred’, and one in Group B whose event originally ‘occurred’ is changed to ‘did not occur’. The CI of the updated meta-analysis is recalculated after each adjustment (a total of 2n adjustments per iteration). If the resulting CI crosses the null value of 1, the FI is considered to be 1. If not, the change producing a CI with the upper limit closest to 1 is used as the basis for the next iteration. This process is repeated until the CI crosses 1, and the number of iterations required to reach this point is defined as FI.
Data analysis
We grouped the included meta-analyses of vascular surgery published over the past 5 years based on whether the results were statistically significant or not. The characteristics of these meta-analyses were described as follows: continuous data were presented using the median (M), along with the 25th percentile (P25) and 75th percentile (P75), while categorical data were reported as frequencies and proportions.
To describe the overall distribution of FIs in meta-analyses of vascular surgery, a frequency distribution histogram was generated. In addition, we categorised the included meta-analyses based on statistical significance (significant vs non-significant) and outcome type (mortality vs non-mortality). The Mann-Whitney U test was used to compare FIs between groups.
Next, the distribution of FIs was described according to the corresponding research fields of the meta-analyses, to explore the differences in robustness across various research domains.
Finally, RCS was incorporated within two multivariable logistic regression models to investigate the potential non-linear associations of sample size and total number of events, respectively, with the fragility of meta-analyses (reference group: FI≤5). In both models, FI served as the dependent variable.
In the first model, sample size was the primary independent variable, with adjustment for the following covariates: total number of events, model used (fixed-effect vs random-effect), width of CI, I², statistical significance, pooled effect size, method used (DerSimonian and Laird, inverse variance and Mantel-Haenszel (MH)), study field (venous, aortic, peripheral arterial, vascular access and others) and outcome type. In the second model, the total number of events was the primary independent variable and covariates included sample size, model used, width of CI, I², statistical significance, pooled effect size, method used, study field and outcome type. Covariates were selected based on a literature review6 7 9 to ensure adequate control for confounding. To further evaluate the robustness of the results, sensitivity analyses were performed using an alternative FI threshold (reference group: FI≤4) and the entire modelling process was repeated. Additionally, to assess the influence of methodological choices related to heterogeneity, a subgroup analysis stratified by model type (fixed-effect vs random-effect) was performed, allowing direct comparison of associations under different synthesis assumptions.
Except for the FI calculation, all analyses and visualisations were performed using R Project V.4.4.3. All tests were two-sided, with a significance level of α=0.05.
Results
Study characteristics
A total of 7453 studies were retrieved. After deduplication and screening, 67 studies were included in the final analysis. 43 of them were from cardiovascular journals (eg, Journal of the American Heart Association, European Journal of Vascular and Endovascular Surgery). 18 were from general medical journals (eg, eClinicalMedicine). And six were from journals of other fields (eg, Renal Failure). The literature screening process was presented in online supplemental figure A1 and the list of included studies was shown in online supplemental table A3. The included studies were relatively evenly distributed from 2019 to 2025, with approximately 10 studies per year.
The characteristics of the 291 included meta-analyses were shown in table 1. Notably, none of the studies reported using the FI to assess the robustness of their findings. 118 meta-analyses were statistically significant. The median number of RCTs included in each meta-analysis was 4, with a median sample size of 805 participants and a median number of events of 142. The median I² was 4%. Most meta-analyses focused on venous or peripheral arterial diseases. Outcomes involving mortality accounted for 22.34% of all included comparisons. The majority of studies reported effect measures as OR or RR, with the MH used for pooled estimation. Most studies employed a random-effects model, and the vast majority of studies did not receive funding support.
Characteristics of included meta-analyses
Distributions of Fragility Index
The frequency distribution histogram of FIs was shown in figure 1. The overall distribution of FIs of vascular surgery was positively skewed (figure 1A), with most meta-analyses below 20. The median of FIs was 7 (4, 15), with a minimum of 1 and a maximum of 591. Meta-analyses with an FI greater than 5 accounted for 58.08%, indicating that more than half of included meta-analyses were relatively robust.
The frequency distribution histogram of FI. FI, Fragility Index.
The overall distributions of FIs for statistically significant and non-significant meta-analyses (figure 1B) were both positively skewed. For statistically significant meta-analyses, most FIs were below 20, with the median 8 (3, 24), a minimum of 1 and a maximum of 591. For non-statistically significant meta-analyses, most FIs were below 10, with the median 7 (4, 12), a minimum of 1 and a maximum of 132. The FI greater than 5 was observed in 55.08% of the statistically significant and 60.12% of the non-statistically significant, indicating that more than half of the meta-analyses were relatively robust. The Mann-Whitney U test showed no statistically significant difference in the distribution of FIs between the two groups (U=8946.50, p=0.073).
The overall distributions of FIs mortality outcome meta-analyses and non-mortality meta-analyses (figure 1C) were both positively skewed. For mortality outcome meta-analyses, most FIs were below 20, with the median 9 (5, 17.50). For non-mortality outcome meta-analyses, most FIs were below 15, with the median 6 (3, 14). The FI greater than 5 was observed in 69.23% of the mortality outcome meta-analyses and 54.87% of the non-mortality outcome meta-analyses, indicating that more than half of the meta-analyses were relatively robust. The Mann-Whitney U test showed a statistically significant difference in the distribution of FIs between the two groups (U=6033.00, p=0.028), indicating that FIs in the mortality outcome group were higher than those in the non-mortality outcome group.
Distributions of Fragility Index in different research fields
The research fields of the included meta-analyses were categorised into five groups: venous, aortic, peripheral arterial, vascular access and others. Distributions of FIs across these fields were shown in figure 2. For the venous, the median of FIs was 6 (3, 14), with a minimum of 1 and a maximum of 97. For the aortic, the median of FIs was 9 (5, 16), with a minimum of 2 and a maximum of 166. For the peripheral arterial, the median of FIs was 8.5 (4, 21), with a minimum of 1 and a maximum of 591. For the vascular access, the median of FIs was 6 (3, 10), with a minimum of 1 and a maximum of 72. For the others, the median of FIs was 7 (4, 14), a minimum of 1 and a maximum of 67.
Distribution of FI in different research fields. FI, Fragility Index.
Correlation between Fragility Index and sample size, total number of events
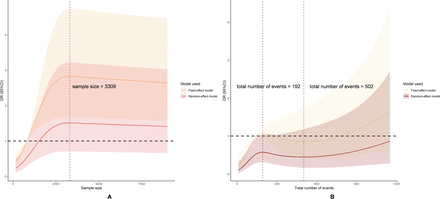
The RCS analysis of all meta-analyses was shown in figure 3. The relationship between sample size and FI was illustrated in figure 3A, showing a non-linear association. When the sample size was less than 3309, the robustness of the meta-analyses increased with increasing sample size. However, when the sample size exceeded 3309, the robustness decreased as the sample size continued to increase.
Using restricted cubic spline to explore the correlation between Fragility Index and sample size (A), total number of events (B).
The relationship between the total number of events and the FI was shown in figure 3B, also demonstrating a non-linear pattern. When the total number of events was less than 192, robustness increased as the total number of events increased. Between 192 and 502, robustness declined. When the total number of events exceeded 502, the robustness again increased with the number of events.
The sensitivity analysis results were shown in online supplemental figure A2. The robustness of the meta-analysis exhibited a non-linear relationship with both sample size and total number of events. For sample size (online supplemental figure A2A), robustness continuously increased as sample size increased. However, the rate of increase markedly declined when the sample size exceeded 3000. For the total number of events (online supplemental figure A2B), the relationship with robustness initially increased, then decreased and finally increased again. Overall, the results of this analysis were relatively robust.
Subgroup RCS analyses stratified by model used (fixed-effect vs random-effect) were shown in figure 4, which illustrated similar non-linear associations between sample size or total number of events and FI. The trends of curves were largely parallel and their 95% CI substantially overlapped across the entire range, suggesting no significant interaction by model used. Notably, RCS curves for the fixed-effect model subgroup were consistently higher than those for the random-effect model subgroup, indicating that fixed-effect model meta-analyses were more robust after adjusting for sample size and total number of events.
Subgroup analysis by outcome type: impact of sample size (A) and event count (B) on Fragility Index.
Discussion
With the rapid increase in meta-analyses of vascular surgery, attention has shifted from quantity to concerns over methodological quality and result robustness. The FI has emerged as a valuable post hoc metric for assessing how easily statistical significance can be overturned by small changes in outcome events.8 12 Unlike power analysis, which evaluates study design adequacy before data collection, the FI examines the vulnerability of significant results after a study has been conducted. Furthermore, different from traditional sensitivity analyses, such as leave-one-out, which assess the influence of individual studies, FI captures event-level fragility and may reveal hidden instability not detectable through study-level assessments.8 The study aimed to systematically assess the robustness of RCT-based meta-analyses in vascular surgery and to investigate key determinants of FI such as sample size and total number of events.
Beyond quantifying fragility, our study aligns with recent findings emphasising broader methodological concerns in meta-analyses of vascular surgery: Javidan et al11 reported that systematic reviews in this field often fall short in adherence to the PRISMA guideline, particularly in protocol registration, search transparency and RoB evaluation. These limitations undermine the interpretability and reliability of pooled evidence. Within this context, the FI should be regarded as a complementary tool, rather than standalone indicators, for evaluating meta-analyses credibility. Notably, although some of the included meta-analyses addressed overlapping clinical questions, none applied the FI, thereby minimising the risk of bias due to topic duplication in the FI distribution.
Our findings revealed considerable variability in robustness across different vascular surgery domains. Meta-analyses focusing on aortic interventions showed the highest median FI of 9, suggesting greater stability, likely due to larger sample sizes and more rigorous trial design. In contrast, studies on venous and vascular access interventions exhibited lower median FI, indicating greater susceptibility to event-level changes.
Further analysis demonstrated that the relationships between FI and both sample size and total number of events were non-linear. While larger sample size generally improved robustness by increasing statistical precision,13 this benefit plateaued beyond a certain threshold (3309). Several explanations are possible. First, large sample size often introduces more heterogeneity,14 especially when multiple trials are involved, undermining pooled effect estimates.15 16 Second, more participants do not necessarily guarantee more events. If the event rate is low, robustness remains limited. In some cases, larger sample sizes with constant event counts may even reduce FI due to shifts in underlying assumptions.17 Third, large samples can increase the risk of statistical over-sensitivity, making it easier to detect small, clinically irrelevant differences and thus inflating false-positive rates.18 Trial Sequential Analysis (TSA) has been proposed as a method to mitigate such errors by adjusting for the required information size.18 Lastly, when heterogeneity is high, larger samples may amplify the impact of publication bias, further reducing result stability.19
Conversely, in meta-analyses with smaller sample sizes, FI exhibited greater fluctuation. This is because in small trials, even a few outcome changes can substantially alter the overall result, leading to statistical fragility.5 In some cases, reversing the event status of just one or two participants was sufficient to change the result statistical significance. This finding emphasises the particular importance of FI in interpreting small-sample meta-analyses, where robustness is especially uncertain.5 20
For the total number of events, a similarly complex pattern emerged. While an initial increase in events typically improved robustness, this effect diminished beyond a certain threshold. Studies in fields such as epilepsy, critical care and paediatrics have shown that a high number of events does not always translate to high FI.21–23 In fact, even studies with hundreds of events sometimes displayed extremely low FIs, reinforcing the notion that robustness is influenced not only by volume of events but also by the distribution and statistical influence.
In summary, the relationship between the FI, sample size and total number of events was complex. While larger sample sizes and more events generally support robustness, exceeding certain thresholds may paradoxically reduce it, especially in the presence of high heterogeneity or low event rates.24 Factors such as study design and potential biases must also be considered when interpreting FI values and their implications for clinical decision-making.
The limitations of this study are as follows. First, this study only includes meta-analyses with dichotomous outcomes and pooled effect measures of OR, RD and RR, and does not evaluate studies with continuous outcomes, network meta-analyses or other types of data. Key vascular surgery outcomes, such as time-to-event data, are also excluded. An important limitation lies in the scope of the FI itself. While FI provides an intuitive measure of statistical robustness, it does not account for between-study heterogeneity, which can significantly affect the interpretation of pooled results. Similarly, publication bias, where negative or null results are under-reported, can distort fragility assessments by inflating the apparent strength of pooled effects. Moreover, the FI is sensitive to the choice of effect measure, and variability in outcome definitions across studies may further limit its comparability. In addition, the RoB of the primary RCTs is not included in the analysis, due to the inconsistent use of quality appraisal tools across meta-analyses, which makes standardised extraction unfeasible. Therefore, the FI should be interpreted cautiously and viewed as part of a broader framework for evaluating robustness, rather than a standalone indicator. Furthermore, this study does not include grey literature, such as unpublished studies and dissertations and only three databases are searched, which may lead to the omission of important research data. Only English-language studies are included, potentially excluding high-quality research conducted in non-English-speaking regions and introducing cultural or regional bias. Finally, most original meta-analyses do not report the number of patients lost to follow-up, which may affect the robustness of the conclusions.
Conclusion
This study systematically assessed the robustness of RCT-based meta-analyses in vascular surgery using the FI as a quantitative measure. The results indicated a moderate level of robustness overall, but significant variability across fields. Aortic studies demonstrate higher robustness, likely due to larger sample sizes and rigorous designs, while venous and vascular access studies exhibit lower FIs, indicating greater fragility. A key finding is the non-linear relationship between FI, sample size and total number of events, whereby increases in these parameters beyond certain thresholds do not always enhance robustness and, in some cases, may reduce it due to increased heterogeneity or a higher risk of false-positive results. Conversely, smaller sample sizes and fewer events are associated with greater fragility, highlighting the importance of improving study quality and minimising heterogeneity in meta-analyses.
Future studies should aim to enhance the methodological quality of meta-analyses by adopting more comprehensive strategies to evaluate robustness. For instance, comparing established appraisal tools such as PRISMA and AMSTAR with fragility-based metrics like the FI could help clarify their alignment and complementarity in assessing evidence quality. Furthermore, developing multidimensional evaluation frameworks that integrate the FI with effect size interpretation, heterogeneity analysis and publication bias assessment may offer a more nuanced understanding of meta-analyses reliability. Incorporating TSA, which adjusts for random error and required information size, could further reduce the risk of false-positive or premature conclusions in cumulative meta-analyses. Additionally, the use of RFI in non-significant meta-analyses may help clarify the robustness of borderline findings. Future frameworks may also consider incorporating structured RoB assessments of primary RCTs, such as using the Cochrane RoB tool, as a covariate to examine whether study-level methodological quality influences fragility outcomes. Collectively, these approaches could support the development of a more holistic and reliable robustness assessment system, ultimately enhancing the interpretability and clinical utility of meta-analysis evidence.
In conclusion, enhancing the robustness and methodological quality of meta-analyses is crucial to ensuring their reliability and clinical applicability. Expanding the use of FI alongside established quality assessment tools, and integrating multidimensional evaluation frameworks may promote more consistent, reliable and actionable findings, thereby supporting evidence-based decision-making in vascular surgery and beyond.
Data availability statement
Data are available upon reasonable request. All data relevant to the study are included in the article or uploaded as supplementary information. All of the data were publicly available data and researchers interested in our study should contact the corresponding author at guoyi0426@qq.com by providing specific ideas.
Ethics statements
Patient consent for publication
Ethics approval
Not applicable.
References
Footnotes
JL and YG contributed equally.
Contributors YG concepted and designed the study. LL, JW, GC and QH searched the databases. JL, CW and YG conducted the literature selection. TW and WL extracted data. YG conducted statistical analysis. JL, YG, CW, TW, WL, LL, JW, GC and QH wrote the original draft. JL, YG, CW and TW reviewed and edited the article. YG is responsible for the overall content as guarantor.
Funding This work is supported by the National Natural Science Foundation of China (82300542) and Quzhou Key Science and Technology Project (No.2022K49).
Competing interests None declared.
Patient and public involvement Patients and/or the public were not involved in the design, or conduct, or reporting, or dissemination plans of this research.
Provenance and peer review Not commissioned; externally peer reviewed.
Supplemental material This content has been supplied by the author(s). It has not been vetted by BMJ Publishing Group Limited (BMJ) and may not have been peer-reviewed. Any opinions or recommendations discussed are solely those of the author(s) and are not endorsed by BMJ. BMJ disclaims all liability and responsibility arising from any reliance placed on the content. Where the content includes any translated material, BMJ does not warrant the accuracy and reliability of the translations (including but not limited to local regulations, clinical guidelines, terminology, drug names and drug dosages), and is not responsible for any error and/or omissions arising from translation and adaptation or otherwise.